理解 box-shadow
首先,回顾一下 box-shadow 这个属性。基本属性用法就是给元素创造一层阴影。
再简单提一下,本文会用到的关于阴影的第一个技巧:
使用阴影复制图像/投影图像
当 box-shadow 的第三、第四个参数模糊半径和扩张半径都为 0 的时候,我们可以得到一个和元素大小一样的阴影:
div {
width: 80px;
height: 80px;
border: 1px solid #333;
box-sizing: border-box;
box-shadow: 80px 80px 0 0 #000;
}得到如下结果:
阴影可以是多重的
第二个技巧则是,box-shadow 是允许多重阴影的,并且他们的坐标是可以完全掌控的。
是的,我们可以像下面这样给一个元素定义多重阴影,并且利用阴影的第一、第二个参数控制它相对于元素的坐标:
div {
width: 80px;
height: 80px;
border: 1px solid #333;
box-sizing: border-box;
box-shadow: 80px 80px 0 0 #000, 70px 70px 0 0 #000, ... 60px 60px 0 0 #000;
}在阴影坐标中运用三角函数
继续。接下来,我们尝试在阴影的坐标中引入三角函数。
为啥是三角函数,不是圆的标准方程或者椭圆的标准方程或者其他图形函数呢?当然也是可以的,只是这里借助三角函数的 cos 或 sin 可以实现直接使用 CSS 实现起来很困难的曲线。
带着疑问,先继续向下,假设我们要实现这样一条曲线:
使用 CSS 的话,有什么办法呢?
可能的一些办法是 clip-path,或者一些奇技淫巧,使用 text-decoration 里的波浪下划线 wavy,或者是使用渐变叠加。
当然,还有一种办法是本文将提到的使用 box-shadow 及 三角函数。
三角函数
咳咳,简单回顾下三角函数里面的 sin、cos 曲线图像变换,还没有全部还给老师。
如果我们有一个 1x1 的 div,它的多重阴影,能够按照像正弦/余弦函数的图像一样进行排布,连起来不就是一条曲线吗?
如何在 CSS 中使用三角函数 sin/cos
想法不错,但是 CSS 本身并没有提供三角函数。这里,我们需要借助 Sass 来在 CSS 中实现简单的三角函数。
还好,已经有前人帮忙把这个工作做完了:
简单而言,就是借助三角函数的泰勒展开式,使用 Sass 函数模拟实现三角函数的 sin()、cos()、tan():
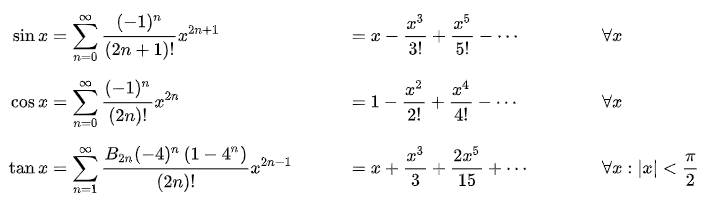
由于展开式是无限长的,使用 Sass 函数模拟时,不可能得到一个非常精确的值,但是在日常作图下已经完全够用了,以下是使用 Sass 函数模拟实现三角函数的 sin()、cos()、tan():
@function fact($number) {
$value: 1;
@if $number>0 {
@for $i from 1 through $number {
$value: $value * $i;
}
}
@return $value;
}
@function pow($number, $exp) {
$value: 1;
@if $exp>0 {
@for $i from 1 through $exp {
$value: $value * $number;
}
} @else if $exp < 0 {
@for $i from 1 through -$exp {
$value: $value / $number;
}
}
@return $value;
}
@function rad($angle) {
$unit: unit($angle);
$unitless: $angle / ($angle * 0 + 1);
@if $unit==deg {
$unitless: $unitless / 180 * pi();
}
@return $unitless;
}
@function pi() {
@return 3.14159265359;
}
@function sin($angle) {
$sin: 0;
$angle: rad($angle);
// Iterate a bunch of times.
@for $i from 0 through 20 {
$sin: $sin + pow(-1, $i) * pow($angle, (2 * $i + 1)) / fact(2 * $i + 1);
}
@return $sin;
}
@function cos($angle) {
$cos: 0;
$angle: rad($angle);
// Iterate a bunch of times.
@for $i from 0 through 20 {
$cos: $cos + pow(-1, $i) * pow($angle, 2 * $i) / fact(2 * $i);
}
@return $cos;
}
@function tan($angle) {
@return sin($angle) / cos($angle);
}由于上面最终计算 sin、cos 泰勒展开的时候,只使用了 20 层循环,所以当传入的值太大的时候,则会产生较大误差。经测试,传入数值在 [-20, 20] 以内,精度还是非常高的。
而以 sin 函数为例,x 取值在 [-π, π] 之间,已经能覆盖所有 sin(x) 的取值范围,所以 [-20, 20] 这个范围是完全够用的,我们只需要尽量让传入的 x 值落在这个区域范围内即不会产生太大误差。
好,铺垫了那么多,接下来使用上述的 sin 函数试一下,假设我们有这样一个结构:
<div></div>div {
width: 1px;
height: 1px;
background: #000;
border-radius: 50%;
}我们再借助 Sass 实现一个 50 层的循环,当然其中阴影的 x 坐标使用了 sin 函数:
@function shadowSet($vx, $vy) {
$shadow: 0 0 0 0 #000;
@for $i from 0 through 50 {
$x: sin($i / 8) * $vx;
$y: $i * $vy;
$shadow: $shadow, #{$x} #{$y} 0 0 rgba(0, 0, 0, 1);
}
@return $shadow;
}
div {
width: 1px;
height: 1px;
background: #000;
border-radius: 50%;
box-shadow: shadowSet(4px, 1px);
}上面 sin($i / 8),这里除以 8 是为了让整个 sin(x) 传入的作用域的取值范围为 [0, 6.25],当而 sin(x) 的作用域为 [0,2π] 时刚好可以画一条完整的单次曲线。这个 8 是可以根据循环的次数不同而进行调整的。
实际,我们得到的 box-shadow 如下:
{
box-shadow: 0 0 0 0 black, 0.4986989335px 1px 0 0 black,
0.989615837px 2px 0 0 black, 1.4650901163px 3px 0 0 black,
1.9177021544px 4px 0 0 black, 2.3403890918px 5px 0 0 black,
2.7265550401px 6px 0 0 black, 3.0701740089px 7px 0 0 black,
3.3658839392px 8px 0 0 black, 3.6090703764px 9px 0 0 black,
3.7959384774px 10px 0 0 black, 3.9235722281px 11px 0 0 black,
3.9899799464px 12px 0 0 black, 3.9941253622px 13px 0 0 black,
3.9359437875px 14px 0 0 black, 3.8163431264px 15px 0 0 black,
3.6371897073px 16px 0 0 black, 3.4012791593px 17px 0 0 black,
3.1122927876px 18px 0 0 black, 2.7747401278px 19px 0 0 black,
2.3938885764px 20px 0 0 black, 1.9756811944px 21px 0 0 black,
1.5266439682px 22px 0 0 black, 1.0537839735px 23px 0 0 black,
0.5644800322px 24px 0 0 black, 0.0663675689px 25px 0 0 black,
-0.4327805381px 26px 0 0 black, -0.9251752496px 27px 0 0 black,
-1.4031329108px 28px 0 0 black, -1.8591951521px 29px 0 0 black,
-2.286245275px 30px 0 0 black, -2.677619305px 31px 0 0 black,
-3.0272099812px 32px 0 0 black, -3.3295620582px 33px 0 0 black,
-3.5799574329px 34px 0 0 black, -3.7744887692px 35px 0 0 black,
-3.9101204707px 36px 0 0 black, -3.9847360499px 37px 0 0 black,
-3.9971711559px 38px 0 0 black, -3.9472317429px 39px 0 0 black,
-3.8356970987px 40px 0 0 black, -3.6643076841px 41px 0 0 black,
-3.4357379737px 42px 0 0 black, -3.1535547213px 43px 0 0 black,
-2.8221613023px 44px 0 0 black, -2.446729px 45px 0 0 black,
-2.03311631px 46px 0 0 black, -1.58777752px 47px 0 0 black,
-1.1176619928px 48px 0 0 black, -0.630105724px 49px 0 0 black,
-0.1327168662px 50px 0 0 black;
}实际得到的图像如下:
控制颜色及初始方向
看看上面 Sass 实现的这个方法 @function shadowSet($vx, $vy) ,其中 $vx,$vy 用于控制图像的振幅及松散程度,我们再添加一个控制初始方向的 $direction,控制阴影层数的 $count, 控制颜色的 $color:
@function shadowSet($vx, $vy, $direction, $count, $color) {
$shadow: 0 0 0 0 $color;
@for $i from 0 through $count {
$x: sin($i / 8) * $vx * $direction;
$y: $i * $vy;
$shadow: $shadow, #{$x} #{$y} 0 0 $color;
}
@return $shadow;
}.line {
width: 1px;
height: 1px;
margin: 10vh auto;
background: #000;
border-radius: 50%;
box-shadow: shadowSet(4px, 1px, 1, 50, #000);
}
.reverseline {
width: 1px;
height: 1px;
margin: 10vh auto;
background: #000;
border-radius: 50%;
box-shadow: shadowSet(8px, 2px, -1, 100, red);
}控制颜色
再进一步,我们可以借助 Sass 的各种颜色函数,实现颜色的变化:
@function shadowSetColor($vx, $vy, $direction, $count, $color) {
$shadow: 0 0 0 0 $color;
@for $i from 0 through $count {
$color: lighten($color, 0.5);
$x: sin($i / 8) * $vx * $direction;
$y: $i * $vy;
$shadow: $shadow, #{$x} #{$y} 0 0 $color;
}
@return $shadow;
}
.colorline {
width: 5px;
height: 5px;
margin: 10vh auto;
background: green;
border-radius: 50%;
box-shadow: shadowSetColor(8px, 2px, -1, 100, green);
}上面,借助了 lighten 这个函数,通过改变颜色的亮度值,让颜色变亮,创建一个新的颜色。
当然,Sass 中还有很多其他颜色函数:
- adjust-hue($color,$degrees):通过改变一个颜色的色相值,创建一个新的颜色;
- lighten($color,$amount):通过改变颜色的亮度值,让颜色变亮,创建一个新的颜色;
- darken($color,$amount):通过改变颜色的亮度值,让颜色变暗,创建一个新的颜色;
- saturate($color,$amount):通过改变颜色的饱和度值,让颜色更饱和,从而创建一个新的颜色
- desaturate($color,$amount):通过改变颜色的饱和度值,让颜色更少的饱和,从而创建出一个新的颜色;
更多 Sass 颜色函数,可以看看这篇文章:Sass 基础——颜色函数
OK,看看这次的效果:
在 css-doodle 中使用
OK,前面所有的铺垫都是为了在实际的一些创意想法中去使用它。
在 css-doodle 中,由于是利用 Web Component 特性。在需要三角函数的时候,可以直接使用 JavaScript 提供的 Math 函数,会更加的方便。
Web Components 是一套不同的 Web 技术,允许您创建可重用的定制元素(它们的功能封装在您的代码之外)并且在您的 web 应用中使用它们。
袁川老师,也就是 css-doodle 库的作者,在他的 Codepen 首页背景板中,使用的就是使用上述技巧实现的一副纯 CSS 画作:
我也尝试使用这个技巧,做了一副:
